What happens if you have to make a lot of crossovers on a circuit board? For example, here is a printed circuit board that connects pins 1 to 10 in a randomly chosen order. In this layout, finished by a person after the autorouter gave up, you have to drill 14 holes, spend time and create dust.
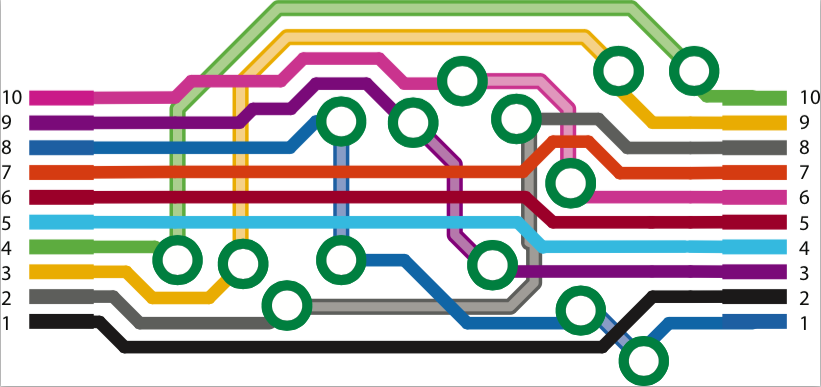
Keeping in mind that our group is working on unconventional electronics, could a woven circuit do better? Woven items are made of crossovers between warp and weft threads. Looking at the problem of how you would bring 10 connectors from right to left on a circuit, crossovers are painless if the wires are insulated, but corners are harder because they involve soldering and cutting. Here is an autorouter in action that draws the same circuit as the PCB, attempts to minimize corners and doesn’t get stuck. (MATLAB code and 100-pin example after the jump).

Here is the code.
%weaveroute
%CKH Aug 2015
%Use the "sliding puzzle" method to route N horizontal threads to their
%randomly chosen destinations by creating a gap
%Check if any lines are crooked
%Move the first crooked line half off its destination to open a gap; the
%penalty for doing this is an extra pair of corners.
%Then use that gap to switch over each crooked line in turn.
%Then plot all those lines, and finally draw in all the straight lines.
%Then, fix any problems where two lines overlapped. Each fix adds an extra
%pair of corners.
clear;
N=10;%How many threads?
Source=1:N; %Here's the original thread positions
Dest=randperm(N); %Here's where I have to route them
Straightline=find(Source==Dest);%get indices of any straight line pairs
Numstraight=length(Straightline);
hold off
Crookedline=find(Source~=Dest);%the rest are mixed up
Numcrook=length(Crookedline);
%ok works except for some overlaps am gonna have to detect each overlap &
%add a corner pair
if Numcrook >0
%if not all straight lines
HalfpathY=[Source(Crookedline(1)), Source(Crookedline(1)), Dest(Crookedline(1))+0.5, Dest(Crookedline(1))+0.5, Dest(Crookedline(1)), Dest(Crookedline(1))];%Create a gap by moving the first crooked one to halfway off its destination
HalfpathX=[0 1 1];%Begin drawing this crooked, gap-creating line.
RestOPathsX=zeros(4,Numcrook-1); %space to hold all the rest of the paths which will have 4 points
RestOPathsY=RestOPathsX; %Just initializing with zeros so Matlab won't warn about array size increasing
Gapdex=find(Dest==Crookedline(1)); %Find gives the source position of the first crooked line
Oldgap=[Source(Crookedline(1))];
%Now we've moved that trace off and can bring the correct trace down to Gapdex and its destination there.
for i=2:Numcrook%all the rest of these paths will have 4 points
Oldgap=[Oldgap Gapdex];%more about this below
RestOPathsX(2:3,i-1)=i;%Set the x-coordinate where each crooked path makes its vertical transition
RestOPathsY(1:2,i-1)=Gapdex;
RestOPathsY(3:4,i-1)=Dest(Gapdex);
Gapdex=find(Dest==Gapdex);%Gets stuck if there is a loop--so bust out if you've been there before
if(ismember(Gapdex,Oldgap))%uh oh been here before
unused=setdiff(Crookedline,Oldgap);
if (unused)%check that we are not done...if we're done, there's nothing IN unused.
Gapdex=unused(1);%If not done just go with the first unused value.
end
end
end
HalfpathX=[HalfpathX Numcrook+1 Numcrook+1 Numcrook+2]; %finish that first path
RestOPathsX(4,:)=Numcrook+2; %add the final x-coord to all other crooked paths
plot(HalfpathX,HalfpathY,'ko-'); %plot the first path in black
hold on;
plot(RestOPathsX,RestOPathsY,'o-'); %and the remaining crooked paths in various colors
end
StraightPathsX=[];
StraightPathsY=[];
if Numstraight>0
StraightPathsX=repmat([0;Numcrook+2],1,Numstraight);
StraightPathsY=[Source(Straightline);Dest(Straightline)];
plot(StraightPathsX,StraightPathsY,'o--');%straight paths as various colored dashed lines
end
%Next detect & fix overlaps by moving the more lefterly point up 0.5, then
%back down at the end of the row. It shouldn't hit the black line or the
%straight lines because we don't route the crooked paths along their y-values.
%Overlaps can be detected in the XY arrays. Look for same Y value and
%out-of-order X values.
%If there's an overlap I will create Figure 2 and show the repair.
hold off
RestOPathsYFixed=RestOPathsY;
RestOPathsXFixed=RestOPathsX;
badLocs=[];%thing to hold any bad locations in the x-y coords
for j=1:N
crookedLocToCheck=find(RestOPathsY==j);%check if each row is on a crooked path
if(crookedLocToCheck)
crookedX=RestOPathsX(crookedLocToCheck);
if (find(diff(crookedX)<0))%overlap if not monotonic. There are negative values in the diff.
badLocs=[badLocs;crookedLocToCheck];
disp ('OVERLAP!!!')
j %in what row?
end
end
end
%Now I'm going to add a couple points to the offending crooked lines using
%badLocs. Add ([0.5 0.5 0 0]') to the existing y-values, do
%something to bring it back down at the end.
YFixIndex=badLocs([1:4:length(badLocs),2:4:length(badLocs)])
RestOPathsYFixed(YFixIndex)=RestOPathsY(YFixIndex)+0.5;
XFixIndex=badLocs([2:4:length(badLocs)]);
RestOPathsXFixed(XFixIndex)=RestOPathsX(XFixIndex)-1;
%Now extend the end for everyone so we hit the target for all modified & unmodified traces, expanding the array
RestOPathsXFixed=[RestOPathsXFixed;RestOPathsXFixed(4,:);RestOPathsXFixed(4,:)+1];
RestOPathsYFixed=[RestOPathsYFixed;floor(RestOPathsYFixed(4,:));floor(RestOPathsYFixed(4,:))];
PathsToRetract=find((RestOPathsYFixed(3,:)-RestOPathsYFixed(6,:))==0);%Gives which of the traces were not zig zagged at the end
RestOPathsXFixed(5,PathsToRetract)=RestOPathsXFixed(4,PathsToRetract);
RestOPathsXFixed(6,PathsToRetract)=RestOPathsXFixed(4,PathsToRetract);%pull back those path ends
figure(2)
hold off
plot(HalfpathX,HalfpathY,'k+-', 'LineWidth',2);%The initial path
hold on
plot(RestOPathsXFixed,RestOPathsYFixed,'+-','LineWidth',2);%The crooked paths modified to avoid overlap
plot(StraightPathsX,StraightPathsY,'+-','LineWidth',2);%The straight paths
axis tight
axis equal
hold off